
- 확률(Probability)의 재정의
- 통계와 통계량(Statistics)
- 샘플링(Sampling)과 확률 변수(Random Variable)
- 확률 함수: cmf / cdf / pmf / pdf
- 선형대수 표시법: Matrix를 왜 쓰는가?
- 데이터와 차원의 표현: 정보의 압축
- 정규분포로 보는 분포(Distribution)의 의미: 분포는 프리셋(preset)이다
- Bernoulli Trial: Binomial, Geometric, Hypergeometric, Negative binomial distribution
- Poisson Process: Exponential, Gamma, Beta distribution
- 추정(Inference): 귀무가설과 대립가설, 유의 수준과 p-value, 신뢰구간(CI)
- 추정(Inference) (2): Pivotal quantity, Student-t, Chi-square, F test and ANOVA table
- Experiment prediction: 회귀분석(Regression Analysis)의 가정(assumptions)과 아이디어
- Appendix
<오늘 포스트는 스마트폰 보다는 태블릿 / 랩탑 등에서 보시기에 좋습니다.>
1. 그게 뭔데 이 10ㄷㅓㄱ아
확률을 함수로 쓰게 된 경위와 그 중요성에 대해선 이미 충분히 빌드업...이 되었으면 좋겠습니다.
또한 앞서 이산 확률 변수(Discrete RV)와 연속 확률 변수(Continuous RV)의 차이도 살펴 보았으니, 바로 함수 notation을 정리해 봐도 충분할 것 같아요.
이번 포스트부터는 오히려 아이디어적인 부분보다는 약속과 계산에 관한 부분이 많을 테니, 이전보다 더 명확하고 받아들이기 쉬우실 수 있겠습니다.
포스트 제목을 보면 아실 수 있듯 확률 함수는 보통 4종류로 구분합니다. CMF, CDF, PMF, PDF가 그것인데, 무슨 확장자 이름도 아니고 뭔가 벽이 느껴지는 것 같은 기분이니 풀네임을 먼저 살펴 보기로 해요.
한국어로 옮겨 놓으면 분명 어디선가 들어보신 말들일 거예요.
C~ : Cumulative, 누적~ / P~ : Probability, 확률~
~M~ : Mass, ~질량~ / ~D~ : Density, ~밀도~
~F : Function, 함수
라는 의미를 담고 있습니다.
즉, 풀어서 말하면
CMF : Cumulative Mass Function, 누적 질량 함수
CDF : Cumulative Density Function, 누적 밀도 함수
PMF : Probability Mass Function, 확률 질량 함수
PDF : Probability Density Function, 확률 밀도 함수
사실 영문을 그대로 번역해 둔 말이다 보니, 보자마자 정확히 의미를 파악하기는 쉽지 않습니다.
하나씩 살펴보도록 할게요.
1-1. CDF / CMF
C~가 붙은 두 친구는 '누적'이라는 의미를 담고 있습니다.
6면 주사위를 한 번 던져서 나온 수를 X라고 한다면,
$$ P(X\leq x)=\frac{x}{6},\;x={1, 2, 3, 4, 5, 6} $$
이처럼 이산 확률 변수(discrete RV)에 대한 확률 누적 함수를 "누적 질량 함수", CMF라고 부릅니다.
비슷하게, 확률 변수가 연속 확률 변수(continuous RV)라면 그에 대한 확률 누적 함수를 "누적 밀도 함수", CDF라고 합니다.
누적 함수 CMF와 CDF는 \(F_X(x)\)로 표시합니다.
이 노테이션에서 알 수 있듯, 누적 함수는 어떤 함수 f(x)의 합, 혹은 적분을 나타냅니다.
CMF : \(F_X(x)\;=\; \Sigma_X f(x)\)
CDF : \(F_X(x)\;=\;\int_Xf(x)dx\)
누적 함수는 확률을 차곡차곡 쌓아 만든 함수이기 때문에, 우상향하는 모양을 하고 있습니다.
또한 확률의 범위에 의해, 반드시 0과 1 사이의 값을 갖게 됩니다. 즉,
$$ \lim_{x \to \infty}F_X(x)\;=\;1$$
$$\lim_{x \to -\infty}F_X(x)\;=\;0$$
앞서 예시로 들었던 6면 주사위의 CMF를 보면, X가 1보다 작을 때는 항상 함숫값이 0이고, X가 6보다 클 때는 항상 함숫값이 1입니다.

그렇다면 누적 함수를 구하기 위해 사용되는 f(x)가 뭘까요?
1-2. PDF / PMF
확률 함수는 그야말로 확률을 나타내는 함수입니다.
6면 주사위를 던져서 나온 수를 X라고 한다면,
$$ P(X=x)=\frac{1}{6},\;x={1, 2, 3, 4, 5, 6}\;=\;f_X(x) $$
이처럼 이산 확률 변수(discrete RV)에 대한 확률 함수를 "확률 질량 함수", PMF라고 부릅니다.
확률 함수는 꽤나 직관적입니다.

확률의 합은 1이 되기 때문에, pmf의 모든 점의 함숫값을 더하면 1이 됨을 알 수 있겠습니다.
즉, 각 점의 함숫값은 반드시 0과 1 사이에 존재하겠군요.
그럼 비슷하게, 연속 확률 변수의 확률 함수, pdf 역시 생각해 볼 수 있겠습니다.
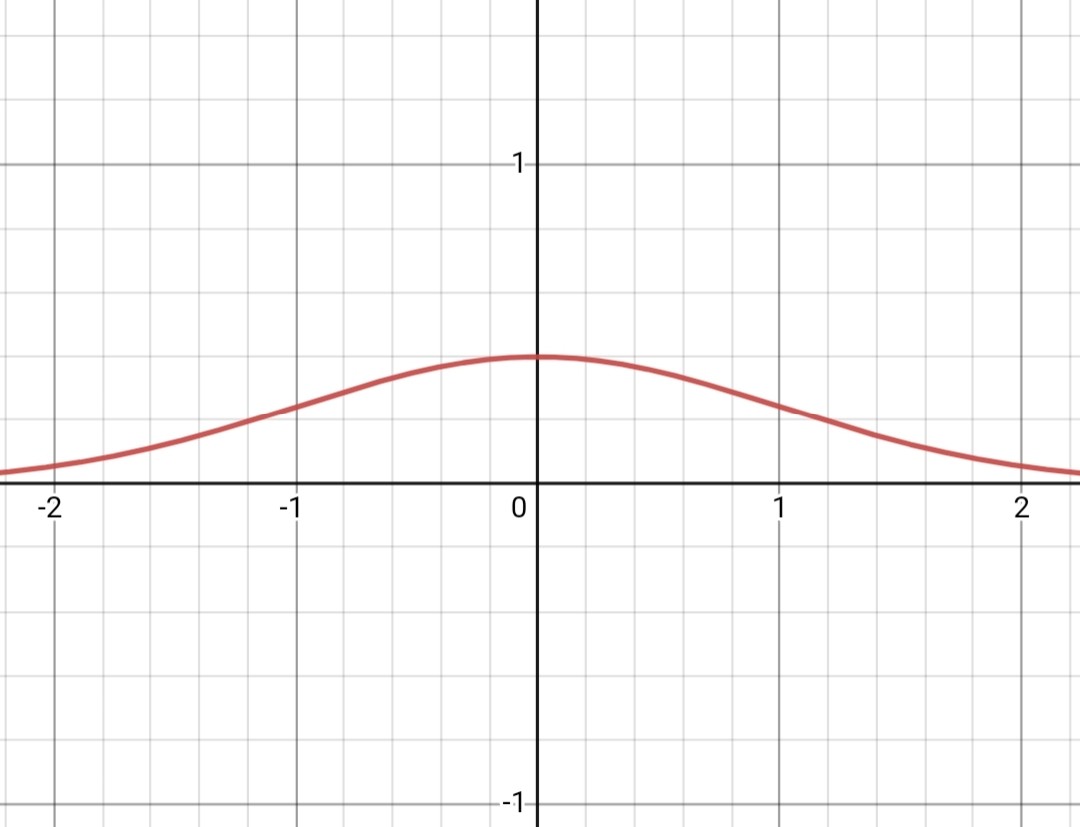
마찬가지로 함숫값이 의미하는 건 그 x값에 해당하는 확률값이겠군요.
라고 생각하면 약간 오산입니다. pmf와 달리 pdf의 함숫값은 확률을 이야기하는 게 아니예요.
직관적으로, 위 정규분포를 따르는 모집단에서 딱 한개의 숫자를 뽑아낸다고 가정했을 때 그 숫자가 0일 확률을 생각해 봅시다.
정규분포의 특성 때문에, 모집단에서 나올 수 있는 숫자는 음의 무한대부터 양의 무한대까지, 유리수든 무리수든 뭐든 나올 수 있습니다.
그중에서 우연히 집은 단 하나의 숫자가 0.00000000...1도 아니고 -0.0000000...1도 아닌 정확히 0일 확률은, 단순히 생각해봐도 거의 없다고 보는 게 맞을 것 같습니다.
아니 그럼 함숫값이 의미하는 게 뭔데?
위와 같은 이유 때문에 연속 확률 변수의 확률은 P(X=x)와 같은 방식으로 이야기하지 않습니다.
셀 수 없이 많은 가능성 속에서 정확히 'x'를 고를 확률은, 대충 0이라고 생각하셔도 무방해요.
대신 연속 확률 변수의 확률은 '구간의 확률'로 이야기합니다. 즉, P(a<x<b) 와 같은 방식으로 이야기해요.
pdf 함숫값은 이 구간의 넓이를 결정합니다.
이렇듯 각 점에서의 확률을 나타내는 게 아닌, 구간의 넓이를 이야기할 때 사용되는 함수이기에 이 확률 함수는 '확률 밀도 함수'라고 불리게 됐습니다.
$$ P(a\leq X\leq b)=\int_a^b f_X(x)\;dx $$
이해를 위해 예시를 하나 가져 올게요.

만약 pdf의 함숫값이 확률을 의미한다면, 위 그래프는 확률 함수가 아닐 겁니다. 함숫값이 1보다 크니까요!
마찬가지로 만약 pdf의 함숫값이 확률을 의미한다면,

얘는 확률이라고 말할 수 있지 않을까요? 함숫값이 1보다 아래 있으니까요.
확률이라면 모든 사건의 확률 합이 1이 되어야겠죠. 연속함수의 사건 확률 합을 어떻게 구할 수 있을까요?
0부터 함숫값 아래의 길이가 각 점에서의 확률일 테니까, 그 선들을 무수히 많이 그려서 보면 되지 않을까요? 아래처럼 말이죠.

어, 이거 고등학교 수학시간에 봤는데.
파란 선들이 무수히 많아진다면, 결국 확률의 합은 pdf 그래프 아래쪽의 넓이와 같다는 걸 알 수 있습니다.
즉, 확률 합은 함수의 리만적분(우리가 고등학교때 배운 그것입니다)을 취한 것이라고 얘기해 볼 수 있겠어요.
$$ \int_0^3f(x)dx $$
이제 1번과 2번의 확률 합을 생각해 봅시다.
1번 직사각형의 넓이는 2 곱하기 0.5 = 1,
2번 직사각형의 넓이는 0.5 곱하기 3 = 1.5.
따라서 1번이 확률 함수가 맞고, 2번이 확률 함수가 아니게 됩니다 (1번이 확률의 공리를 모두 만족하기 때문이예요).
1번 그래프에서 함숫값이 2더라도, 그 점에서 리만 적분 직사각형의 가로 길이가 무한소이기 때문에, 어느 한 점에서 확률은 0이라고 생각하는 거예요.

2. 기댓값, 분산, 공분산
이제 본격적으로 통계학이라는 걸 보도록 해요.
지난 포스트에도 언급했듯, 통계학 분야에서반 배타적으로 사용하는 수학적 연산이 있습니다.
그들 중 가장 기초가 되고 널리 쓰이는 기댓값, 분산, 공분산이 어떤 것이며, 우리에게 무얼 말해주는지 살펴보아요.
2-1. 기댓값은 '가중 평균(Weighted average)' 이다 : E(X)
기댓값을 쉽게 생각하면 '평균' 입니다.
아 그럼 왜 굳이 기댓값이라고 부르는데?
전에도 언급드린 적이 있는 것 같은데, 통계학은 '미래'를 이야기하는 분야입니다. 예측에 가장 큰 목적이 있어요.
평균과 기댓값의 차이는 여기서 나옵니다.

평균은 단순히 우리가 들고 있는 과거의 데이터로부터 뽑아낸 값이고,
기댓값은 미래의 현상을 예측하는 의미가 내포된 말입니다.
미래의 어떤 일을 예측한다면, 우리가 '대충 평균적인 일이 많이 일어나겠지' 라는 생각으로 사용하는 통계량이 평균이라는 정도로 이해하시면 부족하지 않을 것 같습니다.
그래서 기댓값을 'Expectation'이라는 단어로 부르고, 기호로는 이를 줄인 \( E(X) \)를 사용합니다.
평균을 계산하는 방법은 모두 잘 알고 있습니다만, 의미를 좀 뜯어보도록 할게요.
주사위를 한 번 던질 때 나오는 숫자의 기댓값은
$$ E(X)\;=\;\frac{1+2+3+4+5+6}{6}\;=\;3.5$$
우리는 당연하게 분모에 6을 집어 넣었습니다. 왤까요? 전체 사건의 개수가 6개라서?
주사위에서 6 눈을 지워 볼게요. 그리고 그 자리에 3을 하나 더 넣겠습니다. 그럼 평균은 아래처럼 바뀔 거예요.
$$E(X)\;=\;\frac{1+2+3+3+4+5}{6}\;=\;3$$
위와 아래의 차이점이 뭘까요? 아래 식에서는 전체 경우의 수 6가지 중에 3이 나올 경우의 수가 2가지라서 한번 더 더해준 것 같네요.
다시 쓰면 이렇게 바뀔 것 같습니다.
$$E(X)\;=\;\frac{1}{6}\times1\;+\;\frac{1}{6}\times2\;+\;\frac{2}{6}\times3\;+\;\frac{1}{6}\times4\;+\;\frac{1}{6}\times5$$
즉,
\(E(X)\;=\;\)(이벤트 A가 일어날 확률)\(\times\)(이벤트 A) \(+\) (이벤트 B가 일어날 확률)\(\times\)(이벤트 B) \(+\) ...
어렵게 썼지만, 간단하게 전체 sample space 안에 특정 사건 A의 확률이 높다면, 그 일이 다른 사건보다 잘 일어날 것이라고 예상할 수 있다는 말입니다. 이렇게 각 사건의 가중치(weight)를 고려해서, 기댓값은 아래와 같이 정의합니다 :
만약 X가 discrete random variable 이라면,
$$ E(X)=\sum_{X} xf(x)$$
X가 continuous random variable 이라면,
$$ E(X)=\int_X xf(x)\;dx$$
여기서 \(f(x)\)로는 각각 pmf와 pdf를 사용합니다.
정리하자면, 기댓값은 '존재하는 모든 사건들의 가중평균' 정도로 생각하시면 충분할 것 같습니다.
+.
추가로 평균의 계산에 대해서 한가지만 보도록 할게요.
우리가 continuous RV인 X에 대한 확률 함수인 \(f_X(x)\)를 알고 있다고 할 때,
\(g(X)\)의 평균은 다음과 같이 계산합니다 :
$$\int_Xg(x)f_X(x)\;dx$$
g(X)에 대한 확률함수를 넣는 게 아닌가요? 라고 할 수 있겠지만, 그럼 확률 함수 앞에 곱해주는 변수가 g(X)가 아닌 Y( =g(X) )가 되어야 맞겠습니다. 이와 같은 변수의 변환같은 경우는 기회가 되면 다뤄보도록 하겠습니다.
간단한 예시로, g(X)=3X+2 의 평균은 아래와 같이 계산합니다 :
$$E(3X+2)=\int_X(3x+2)f_X(x)\;dx$$
그런데 적분의 특성에 의해 이 식은 이렇게 다시 쓸 수도 있습니다 :
$$\begin{aligned}
E(3X+2)&=3\int_X xf_X(x)\;dx+2\int_Xf_X(x)dx\\
&=3E(X)+2\quad(\because\;\int_Xf(x)dx=1)
\end{aligned} $$
일반화 하면 아래 등식도 성립합니다 :
$$E(aX+b)=aE(X)+b $$
이러한 성질을 기댓값의 " Linearity " 라고 부릅니다. 알아두시면 꽤나 여기저기서 유용하게 쓰일 거예요.
2-2. 분산은 거리다 : Var(X)
지금보다 쪼오오오끔 더 어렸을 때, 교복 입고 다니던 때 배웠던 분산의 의미를 떠올려 볼까요.
정확히 이해는 안갔던 것 같지만, 대충 '우리 데이터가 평균에서 얼마나 떨어져 있는지를 얘기하는 숫자' 와 같은 식으로 설명을 들었던 것 같습니다. 전 이때 '뭐가 얼마나 떨어진건데?' 이런 생각이 들었었어요.
자, 이전에 이런 말씀을 드린 적이 있었던 것 같습니다.
맛보기로 소개하면, 평균과 분산을 계산하는 이유는 'CLT(중심 극한 정리)'를 이용해서 우리 데이터를 '정규 분포로 근사' 시키기 때문입니다. 즉 다른 어려운 모양의 분포를 쉬운 정규분포로 바꿔서 보고자 하기 때문에, 정규분포의 파라미터인 평균과 분산을 사용하는 거예요 (이 부분은 나중에 자세히 다룰 예정이니 일단 추가적인 설명은 넘기겠습니다).
(앞선 포스트에서 복붙한 내용입니다)
다시 말하면, 분산이란 '정규분포의 파라미터' 입니다. 정규분포의 특성을 적용하기 위해 데이터를 잘 조물조물해서 만들어 낸 값이라는 뜻이예요. 그리고 이런 파라미터는 보통 이해의 영역이 아니라 정의의 영역입니다. '앞으로 분산이라는 건 이걸 말하는 거야!' 라고 정해놓은 뒤에, 그걸 갖고서 이것저것 해보자는 거죠.
그럼 분산을 어떻게 정의하는지 따라가 봐요.
정규분포의 모양을 결정하기 위해선 두가지 파라미터가 필요합니다. Location parameter 라고 불리는 평균이 있구요, Scale parameter라고 불리는 분산이 있습니다. 분산은 말 그대로 정규분포가 얼마나 벌어져 있는지, 그 정도를 나타내 주는 숫자입니다. 그걸 좀 정확하게 수치적으로 쓰고 싶어서, 정말 단순하게 분산을 아래와 같이 정의합니다 :
$$ Var(X) = E[\{X-E(X)\}^2] $$
아니 이게 무슨 소리야.
일단 '얼마나 벌어져 있는가' 를 수학적으로 어떻게 쓰면 좋을지 스케치 해봅시다.
두 점이 있다고 치고, 우리는 지금 걔네가 가운데 점으로부터 얼마나 떨어져 있는지 보고 싶다고 해요.

물론 그냥 자를 들고와서 거리를 재보면 간단하긴 하겠지만, 자를 쓸 수 없는 상황이니까 아이디어를 한번 내 볼까요.
일단 좌표를 그리고, 점의 위치를 표시해 봅니다.

그럼 가운데 점부터 각 점까지의 거리를 아래처럼 나타낼 수 있을 것 같습니다.

되짚어 봅시다. 거리를 숫자로 표시하기 위해서 처음으로 한 일은, 출발점 되는 가운데 점을 좌표의 기준, 원점으로 잡은 것이었습니다.
다시 정규 분포로 돌아가서 같은 과정을 생각해 볼까요.

우리가 하고 싶은 일은, 정규분포가 전체적으로 얼마나 퍼져 있는지를 수치로 나타내는 겁니다.
일단 거리를 재려면 원점과 같은 기준이 필요한데, 정규분포에서는 어떤 정보가 원점의 역할을 할 수 있을까요?
우리가 정규분포의 위치 기준으로 사용하는 location parameter, 평균을 기준으로 쓸 수 있겠죠. 평균이 정확히 어디 있는지 우리는 정확한 숫자로 알고 있으니까요.
평균 E(X)를 기준으로, 일단 정규분포 위의 무수히 많은 점들 중 딱 한 점만 골라서 거리를 표현해 봅시다.
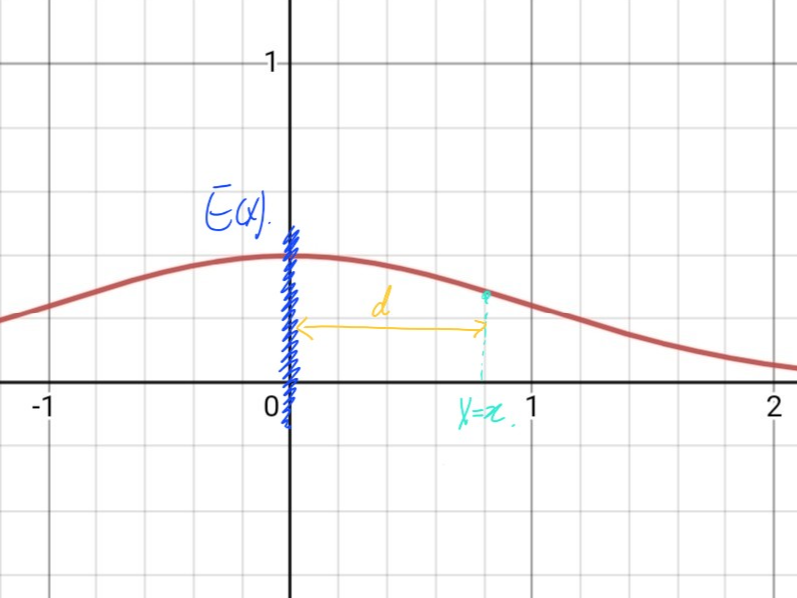
거리 d는 간단하게 x-E(X) 로 쓸 수 있겠습니다.
그런데 만약 우리가 평균의 왼쪽에 있는 점, 그러니까 4사분면 위의 점을 선택했다면 거리는 어떻게 될까요?
'거리' 라는 개념은 양수이니, 반대로 E(X)-x 로 쓸 수 있겠습니다.
이 두 식을 일반화해서, 한줄에 쓸 수 있는 무적의 기호가 있죠. 바로 절댓값입니다.
$$ d=|x-E(X)| $$
어느 특정한 딱 하나의 점에서의 거리는 이렇게 표현할 수 있습니다.
아, 그런데 우리 다들 수능 같은데서 절댓값 보면 안절부절 못하고 불편해하는 병들 있잖아요. 그래서 여기다가 제곱을 해서 절댓값을 없애버리겠습니다.
$$d^2=\{x-E(X)\}^2 $$
이 식이 어느 한 점까지의 거리를 담고 있는 정보입니다.
그러나 우리의 처음 목표는 정규분포가 전체적으로 얼마나 퍼져 있는지 숫자 하나로 나타내는 것이었어요.
저 d 어쩌고 하는 식에, 정규분포의 모든 X들을 대입해서, 딱 하나의 숫자로 깔끔하게 나타낼 수 있는 방법.
그들의 평균을 내면 되겠죠.
$$E(d^2)=E[\{X-E(X)\}^2]$$
그리고 이 식을 우리는 분산(Variance) 이라고 부르기로 했대요.
2-3. 서로 다른 두 놈의 연관성 : Cov(X, Y)
이런 놈은 고등학교 확률과 통계에서 배운 적이 없었는데.
그야 당연합니다. 공분산을 언제 써먹는지 생각해보면 알 수 있어요.
공분산은 두 가지의 변수가 어떤 선형 연관성을 갖고 있는지 설명해주는 녀석입니다. 즉, 변수가 최소한 둘 이상 달린 데이터에서 이야기하는 개념이예요. 여러분이 아직 공간좌표에서 곡면이나 부피로 나타낸 함수를 본 적이 없다면,아직 공분산을 접하지 못하신 게 당연합니다.
간단히만 살펴 보도록 해요. 일단 정의는 아래와 같습니다 :
$$ Cov(X, Y)=E[\{X-E(X)\}\{Y-E(Y)\}] $$
이걸 아래처럼 생각하시면 기억하기 쉬우실 것 같습니다.
$$ Var(X)\;=\; E[\{X-E(X)\}^2] \;=\;E[\{X-E(X)\}\{X-E(X)\}]\;=\;Cov(X,X) $$
이게 우리가 이걸 공분산(Covariance) 이라고 부르는 이유입니다.
공분산같은 경우는 두 데이터의 선형 연관성을 보여줍니다. 값이 0이라면 두 변수는 직선적으로는 연관성이 없다는 걸 말해줘요. 이 말은, 직선이 아닌 모양으로는 관계가 있을 수도 있다는 말입니다. "공분산이 0이다" 와 "두 변수가 서로 관련이 없다" 는 다른 말이라는 것만 챙겨 두시면 좋을 것 같습니다.
또 공분산의 값은 양 음 어느쪽으로든 커질 수 있어요. 절댓값이 클 수록 연관성이 강한 경향이 있는데, 또 데이터가 생긴 것에 따라서 반드시 그런 건 아니라서 연관성의 정도를 비교하고 싶을 땐 보정을 통해 피어슨 상관계수(Pearson-Correlation) 라는 양으로 만들어 주는 편입니다.
\( \vdots \)
라고는 하지만, 사실 저희가 이 시리즈에서 살펴볼 기초 통계학 내용에서는 공분산을 크게 응용할 것 같지는 않습니다. 일단 일변수 함수와 그 분포들에 먼저 익숙해지고 나서야 다른 뭔가를 해볼 수 있을 테니까요.
그러니 적당히 공분산이 양수면 우상향 그래프를, 음수면 우하향 그래프를 그리는 경향성이 있다. 정도로만 생각하고 넘기셔도 좋을 것 같습니다.

이러한 특성에서 예상하실 수 있듯, 공분산은 회귀 분석(Regression Analysis)에서 꽤나 중요하게 다뤄집니다.
3. MGF(적률 생성 함수), 간단히만.
아 이건 또 뭐야. 기초라면서 뭐 이렇게 듣도 보도 못한 것들이 많냐.
처음이라 그렇습니다! 저도 딱 그 생각이었거든요.
사실 원래 계획에는 이 MGF를 부록으로 넣을까 생각했었습니다. 그런데 아무래도 이걸 짚고 넘어가야 이후에 여러가지 분포 이야기를 편하게 할 수 있을 것 같아서, 기초적 내용으로 소개하려고 해요.
우리가 통계를 공부하는 목적은 R을 잘 쓰는 것도, 수학 문제를 잘 푸는 것도 아닌, 데이터 분석을 하기 위함이잖아요.
데이터에서 어떤 경향성을 확인해야 하는데, 제한된 시간과 돈, 샘플 안에서 그런 목적을 달성하려면 있는 것으로부터 분포들 사이의 특성과 관계를 빠르게 파악하는 것도 중요하지 않을까요 (물론 우리가 어떤 데이터를 만날 지는 앞으로 어디서 무슨 일을 하느냐에 따라 천차만별이긴 할 것입니다만).
여튼 MGF라는 이놈, 다소 당황스럽게 생겼고 비전공자 입장에서는 이게 뭐야 싶은 생각도 드는 놈이긴 합니다. 하지만 뒷 이야기를 편하게 하자는 생각으로, 이런게 있다 정도만 소개하도록 할게요. 통계학과 저학년 전공 과목에서는 이거 유도하고 계산하고 외우게 시키지만 그렇게까지 할 필요는 없으니까 부담은 없지 않을까 생각합니다.
MGF, 적률 생성 함수는 아래와 같이 정의합니다 :
X가 continuous RV 라고 가정하면,
$$ M_X(t)\;=\;E[e^{tX}]\;=\;\int_Xe^{tx}f_X(x)\;dx $$
와... 이 짓을 왜 하고 있냐.
3-1. MGF가 왜 MGF인가
MGF의 풀 네임은 'Moment Generating Function' 입니다. 모먼트를 만드는 함수, 대충 모먼트가 적률인가 보네요. 그래서 그게 뭔데.
MGF를 사용하는 첫번째 영역은 평균과 분산을 쉽게 계산하기 위해서 입니다.
일단 한가지 등식을 좀 보여 드릴게요.
X는 변수, E(X)는 연산이 된 딱 하나의 상수입니다.
그리고 앞에서 소개해 드린 기댓값 계산의 linearity를 생각해 보면, 아래 계산을 따라오실 수 있을 것 같습니다.
$$ \begin{aligned}
Var(X) &= E[X-E(X)]^2 \\
&=E[X^2-2XE(X)+\{E(X)\}^2]\\
&=E(X^2)-2E(X)E(X)+\{E(X)\}^2\\
&=E(X^2)-\{E(X)\}^2
\end{aligned} $$
즉, X의 분산은
$$Var(X)=E(X^2)-\{E(X)\}^2 $$
로 쉽게 계산할 수 있습니다.
여기서 MGF의 성질을 하나 소개해 드릴게요.
\(M_X^{(r)}(0)=E(X^r)\), 즉 X의 MGF를 r번 미분한 뒤 t에 0을 대입해서 나오는 숫자는 X의 r제곱의 expectation 입니다.
다시 말해, 우리가 X의 MGF를 알고 있다면
$$Var(X)=M_X''(0)-\{M_X'(0)\}^2 $$
로 쉽게 계산할 수 있습니다. 귀찮게 기댓값 계산한답시고 적분같은 어마무시한 짓을 안할 수 있어요.
여기서, \(X^r\) 과 같이 나타난 형태를 X의 'r th Moments' 라고 부릅니다. MGF가 '모먼츠를 만드는 함수' 라고 불리는 이유가 여기에 있습니다.
물론, 이건 다 MGF를 알고 있을 때의 이야기겠죠. 앞으로 분포들을 살펴볼 때, 그들의 MGF도 함께 소개해 드리도록 하겠습니다.
3-2. MGF는 분포의 지문이다
아직 저희가 아는 분포가 없으니, 간단하게 소개만 드리고 넘어갈게요. 사실 이 얘기를 하려고 MGF 파트를 추가한 것이기도 해요.
굉장히 중요한 성질이니, MGF에 관해서 이 내용은 챙겨 가시면 좋겠습니다.
어떤 변수 X와 Y의 MGF가 같다면, 둘은 같은 분포를 따릅니다.
MGF가 정의 상 확률함수를 변형한 함수니까, 그게 같으면 확률 함수가 같은거 아니냐, 일면 당연해 보이는 소리긴 합니다.
이 성질을 왜 중요하게 말씀드렸느냐. 이걸로 우리는 여러가지 분포의 연결고리를 찾아갈 수 있습니다.
대충 Exponential 분포가 특정한 조건을 만족시키면 Gamma 분포로 쓸 수 있고, Gamma 분포는 또 특정한 조건에서 카이스퀘어(\(\chi^2)\) 분포를 따른다는 걸 이걸로 보여줄 수 있습니다.
즉, 우리가 갖고 있는 어떤 데이터의 형태가 Exponential 분포라는 걸 따르는 모양으로 생겼다면,
그걸 우리는 조물조물해서 카이스퀘어를 따르도록 값을 바꿔줄 수 있고,
카이스퀘어 분포를 이용해서 우리 데이터의 신뢰 구간과 통계적 추정을 할 수 있게 되는 겁니다.
아직은 외계어처럼 읽히시기도 하겠지만 알고보면 어려운 내용이 아니니, MGF가 이런 식으로 응용할 수 있는 발판을 주는구나! 정도로 생각하시면 충분할 것 같습니다.
엄청나게 길었네요! 수식도 많이 들어가고, 수정도 많이 한 파트였습니다.
중반부 포스트는 앞으로 이야기할 여러가지 통계적 내용의 기반이 되는 언어에 익숙해지는 내용으로 계획하고 있습니다.
그래서 다음 시간엔 행렬, Matrix에 관한 내용을 간단하게 들고 와보도록 하겠습니다. 선형대수학이 아니라, 행렬에 관한 내용을요.
'Z-bio stat > Z-기초통계학' 카테고리의 다른 글
| [Z-bio Stat] 6. 데이터와 차원의 표현: 정보의 압축 (0) | 2022.12.29 |
|---|---|
| [Z-bio Stat] 5. 선형대수 표시법: Matrix를 왜 쓰는가? (0) | 2022.12.22 |
| [Z-Bio Stat] 3. 샘플링(Sampling)과 확률 변수(Ramdom Variable) (0) | 2022.11.20 |
| [Z-Bio stat] 2. 통계와 통계량(Statistics) (0) | 2022.11.07 |
| [Z-Bio stat] 1. 확률(Probability)의 재정의 (0) | 2022.10.30 |



