
- 확률(Probability)의 재정의
- 통계와 통계량(Statistics)
- 샘플링(Sampling)과 확률 변수(Random Variable)
- 확률 함수: cmf / cdf / pmf / pdf
- 선형대수 표시법: Matrix를 왜 쓰는가?
- 데이터와 차원의 표현: 정보의 압축
- 정규분포로 보는 분포(Distribution)의 의미: 분포는 프리셋(preset)이다
- Bernoulli Trial: Binomial, Geometric, Hypergeometric, Negative binomial distribution
- Poisson Process: Exponential, Gamma, Beta distribution
- 추정(Inference): 귀무가설과 대립가설, 유의 수준과 p-value, 신뢰구간(CI)
- 추정(Inference) (2): Pivotal quantity, Student-t, Chi-square, F test and ANOVA table
- Experiment prediction: 회귀분석(Regression Analysis)의 가정(assumptions)과 아이디어
- Appendix
< 이번 포스트는 스마트폰 보다 태블릿, PC 등에서 보시기 편하게 작성되었습니다. >
지난 번에 이어서 이번에는 '포아송 프로세스' 라는 것, 그리고 그로부터 파생되는 몇 가지 확률 분포들을 소개해 드리겠습니다.
1. 포아송 프로세스 (Poisson process) ?
'포아송 분포 (poisson distribution)' 라는 게 무슨 뜻인지는 몰라도, 어디선가 들어보신 분들은 많이 계실 것 같습니다.
포아송 분포는 바이오 분야에서도 꽤나 자주 접할 수 있는 분포인데요, 이는 포아송 분포가 쓰이는 상황 때문입니다.
먼저 한 줄로 소개해드리고 자세히 들어가 보겠습니다.
포아송 분포는 잘 일어나지 않는 사건(rare event)의 발생 확률 분포입니다.
흔히 처음 포아송 분포를 적용하는 예시로 자주 언급되는 것들은 이런 경우들이 있어요.
- 제품 A의 생산 과정에서 결함이 발생할 확률이 0.1%일 때, X개의 제품에 결함이 있을 확률
- 일정 시간동안 자라의 식당을 찾는 손님이 X명일 확률 등
그리고 이런 rare event의 발생과 관련한 여러가지 상황들의 확률 분포를 설명하기 위해, 이를 고안한 수학자 시메옹 푸아송(Siméon Denis Poisson)의 이름을 딴 "포아송 프로세스(poisson process)" 라는 것 부터 출발해 보겠습니다.
여담이지만, 통계학 분야는 가만 보면 이름들을 정말 대충 짓는 것 같습니다.
1-1. 모수화 (Parameterization) 와 포아송 분포
레어 이벤트(rare event)라고 해도 "발생 확률" 의 분포라면, 아니 저번 포스트에서 봤던 베르누이 시행으로 확률을 이야기할 수 있는 것 아닌가요? 베르누이나 바이노미얼 같은 친구들이 있는데 왜 굳이 또 포아송 분포라는 걸 고안해 낸 걸까요?
이 아래 부분은 통계학을 처음 접하시는 분들께는 조금 어렵게 느껴지실 수 있습니다.
단순히 포아송 분포가 뭔지 궁금하신 분들께서는 이 1-1 절을 넘어가셔도 좋겠습니다.
Parameterization(매개변수화, 모수화 ; 맞는 번역인지는 모르겠지만, 영어가 너무 길어서 그냥 이하 '모수화' 라고 부르겠습니다)는 genomics 등 데이터를 빡세게 다루고 가공하는 논문들의 method를 보면 종종 보실 수 있는 단어입니다. 어렵고 연습도 많이 필요한 테크닉이라 단순히만 소개해 드리면 어떤 대상(도형이든, 곡선이든, 곡면이든 무엇이든 될 수 있습니다)에 사용되는 변수를 고쳐서 다르게 표현하는 과정을 말하는데, 변수를 줄여 차원을 줄이기 위해서, 혹은 대상을 더 잘 설명하는 파라미터를 도입하기 위해서 등 여러 목적으로 도입합니다.
물론 저희가 이 테크닉을 지금 연습할 필요는 없습니다. 단순히 포아송 분포가, 이전 포스트에서 봤던 베르누이 시행 내지 바이노미얼 분포를 다르게 쓴 식이라는 걸 소개해 드리고자 언급드렸습니다.
바이노미얼 시행의 파라미터는 시행 횟수 n과 시행의 성공 확률 p였습니다.
$$ X \sim Bin(n, p) ;\quad f_X(x)= \begin{pmatrix}n \\ x \end{pmatrix} p^x (1-p)^{n-x} , \quad x \in \{ 1, 2, ... , n \} $$
만약 어떤 시행의 성공 확률 p가 100만분의 1 이라고 할게요. 이런 시행에 바이노미얼을 씌우려고 보니, 시작도 전에 앞이 캄캄해 집니다. 뭔가 꼼수가 필요할 것 같아요.
아래와 같은 그림을 상상해 볼게요.

발생 확률로 따지면 우리가 너무 힘들어지니까, 발생 횟수에 초점을 맞춰 보겠습니다.
적절하게 시간 축 구간을 쪼개 볼게요.
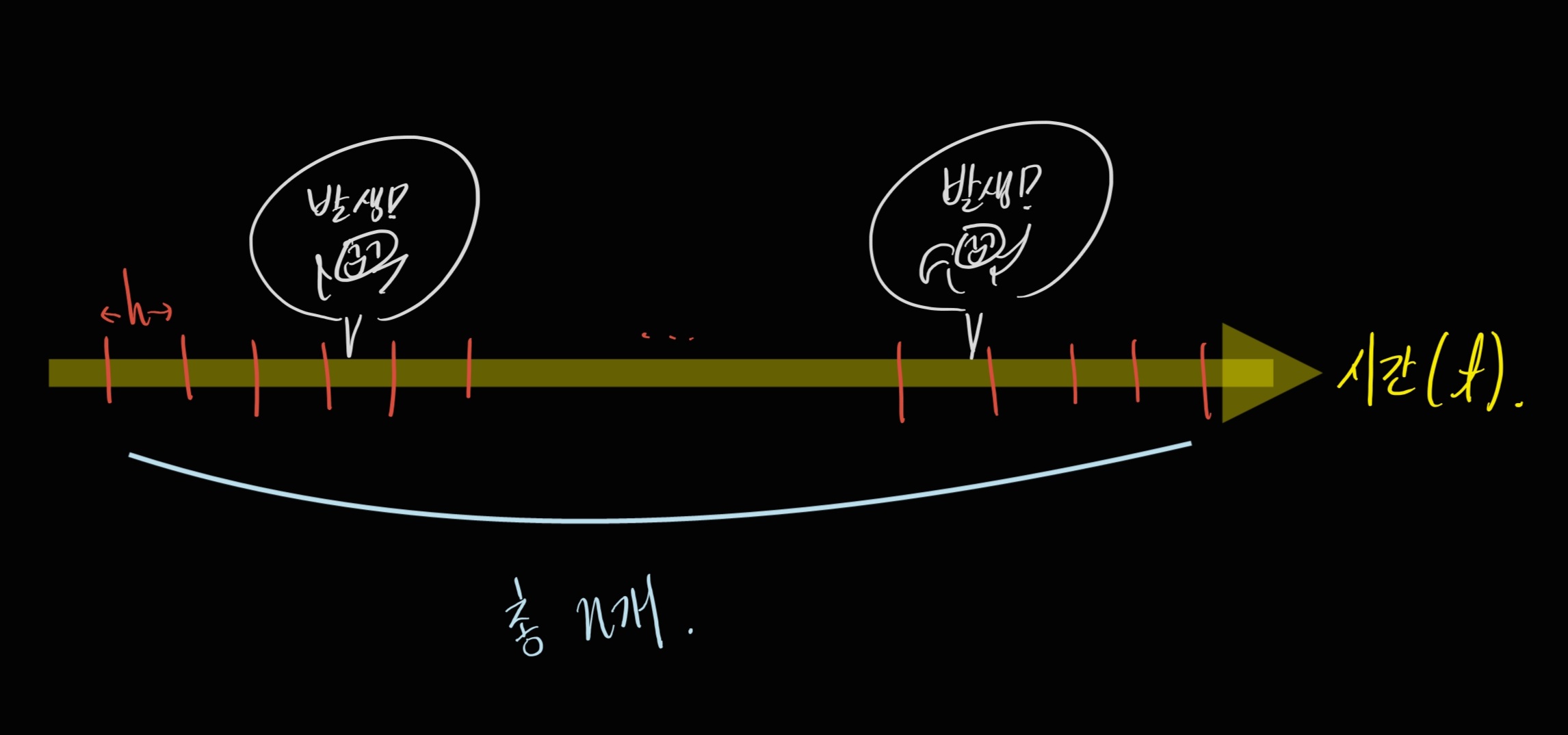
제가 관찰한 t 시간을, 길이가 h로 동일한 n개의 구간으로 쪼개었습니다.
이 때 구간을 나누는 것도 나름대로 규칙이 있습니다:
각 구간에는 이벤트가 발생하지 않거나, 한 번만 발생합니다. 두 번 이상의 이벤트가 한 구간에 몰리지 않도록 나눕니다.
이렇게 적당한 h를 잘 잡은 뒤, 파라미터를 새롭게 써 보겠습니다.
일단 위 그림의 상황은 아래처럼 두 가지 말로 쓸 수 있을 거예요,
- 성공 확률이 p인 시행을 총 n번 했을 때 두 번 성공. 즉, np=2
- 단위 시간 당 발생 횟수가 \( \lambda \)인 사건을 t 시간 만큼 관찰했을 때 두 번 발생. 즉, \( \lambda t \)=2
베르누이 시행으로 이 상황을 바라본 윗줄에서, "어떤 단위 시간 당 발생 횟수" 를 나타내는 새로운 파라미터 람다(\( \lambda \) ) 를 도입한 아랫줄과 같이 같은 상황을 다른 말로 바꾸어 적어 보았습니다. 람다의 기준이 되는 '어떤 단위 시간' 은 정하기 나름이예요. 그러니까,
- 자라네 가게에 10분마다 손님이 한 분씩 온다. 이 때 람다는 1 .
- 자라네 가게에 30분마다 손님이 세 분씩 온다. 이 때 람다는 3 .
- 자라네 가게에 한 시간마다 손님이 여섯 분씩 온다. 이 때 람다는 6 .
이것들은 모두 같은 상황을 나타내지만, 단위 시간을 제 맘대로 정했기 때문에 람다 값이 서로 다릅니다. 그리고 실제로 이들 중 어떤 것을 써도 무방해요. 계산에 제일 적당한 것을 가져다가 쓰면 됩니다.
아무튼 람다가 이런 것을 의미한다고 정했으면, 위 하얀 동그라미의 두 문장을 모든 상황에 대해서 일반화 해 볼 수 있을 거예요.
$$ \begin{aligned} np &= \lambda t \\ \Rightarrow p &= \frac{\lambda t}{n} \end{aligned} $$
이렇게 새로 쓴 p를, 바이노미얼 식에 넣고 정리해 보겠습니다.
$$ \begin{aligned} X &\sim Bin(n, p) \\ \Rightarrow f_X(x) &= \begin{pmatrix}n \\ x \end{pmatrix} p^x (1-p)^{n-x} \\ &= \frac{n!}{x! (n-x)!} \left( \frac{\lambda t}{n} \right)^x \left( 1 + \frac{- \lambda t}{n} \right)^{n-x} \end{aligned} $$
그리고 여기서, 구간의 길이 h를 0으로 보내겠습니다. 구간을 엄청나게 잘게 쪼갠다는 얘긴데, 그러면 구간의 수 n은 무한대로 발산할 거예요 :
$$ h=\frac{t}{n} \Rightarrow n=\frac{t}{h} $$
그러면 우리의 확률 분포 식은 이렇게 정리될 겁니다 :
$$ \begin{aligned} \lim_{n \to \infty} f_X(x) &= \lim_{n \to \infty} \frac{n!}{x! (n-x)!} \left( \frac{\lambda t}{n} \right)^x \left( 1 + \frac{- \lambda t}{n} \right)^{n-x} \\ &= \frac{1}{x!} (\lambda t)^x e^{- \lambda t} \end{aligned} $$
아... 극한 잘 기억 안나는데 무슨 일이 벌어진 걸까요. 다시 한 번 보여 드릴게요.

그리고 마지막으로 남은 저 식은 저희가 새로 정의한 파라미터인 람다로 표현된 확률 함수입니다.
이 때 관찰 시간 t를 한 단위로 보고 1을 넣은 확률 함수를 우리는 "포아송 분포" 라고 불러요.
$$ X \sim Poisson(\lambda) \Rightarrow f_X(x)=\frac{\lambda^x e^{-\lambda}}{x!} $$
또, 편의상 이렇게 시간-구간의 아이디어와 파라미터 람다로 확률을 이야기하는 경우를 "포아송 프로세스(Poisson process)" 라고 말합니다.
1-2. 포아송 분포 (Poisson distribution)
상술드렸듯, 포아송 분포는 바이노미얼 분포를 약간 변형한 확률 함수인데요,
그래서 포아송 분포는 "단위 시간 당 사건의 발생 빈도가 람다일 때, t=1이라는 시간 동안 X번의 사건이 발생할 확률" 을 뜻합니다 (더 정확히는, 1-1에서 \( \lambda t \) 로 적었던 항을 \( \lambda \) 한 글자로 치환해서 썼다고 보는 게 맞지 싶습니다. 위에서 10분, 30분, 60분에 따라 람다 값이 달라지는 게 이걸 의미한다고 받아들여주시면 될 것 같아요).
"X번" 이라는 발생 횟수가 확률 변수이기 때문에, X는 음이 아닌 정수여야 하겠죠.
$$ X \sim Poisson(\lambda) \Rightarrow f_X(x)=\frac{\lambda^x e^{-\lambda} }{x!}, \quad x \in \{ 0, 1, 2, ... \} $$
$$ E(X) = Var(X) = \lambda $$
이 평균과 분산이 모두 파라미터 람다라는 점 때문에 포아송 분포는 여기저기서 유용하게 활용되고 있습니다.
$$ M_X(t)=exp\{ \lambda (e^t -1) \} $$
포아송 분포의 모양은 파라미터 람다에 따라 달라지는데, 람다가 커질수록 정규 분포에 가까워 집니다.
이에 관한 자세한 이야기는 다른 백그라운드가 필요할 것 같으니 다음을 기약하기로 하고, 일단 적당히 "람다가 그럴싸하게 커지면 포아송 분포는 정규 분포로 근사한다" 정도로 받아 들이시면 좋을 것 같습니다.
기초 통계학 과목에서는 다루지 않았던 것 같지만 나름대로 납득이 필요하신 분들을 위해 조금의 힌트를 드리자면, 검정 통계량을 만들 때 자주 꺼내는 "CLT(Central Limit Theorem ; 중심 극한 정리)" 라는 게 있습니다. iid 샘플에서 랜덤하게 뽑은 샘플의 평균은, 샘플 사이즈가 충분히 클 때 정규 분포를 따르게 된다, 라는 이론입니다 (추정 파트에서 다시 한 번 소개해 드리겠습니다).
이전 포스트에서 제가 바이노미얼 분포를 "베르누이 시행의 합" 이라는 개념으로 소개해 드렸던 것 같습니다. 그리고 이 "합" 이라는 건, 랜덤하지 않고 딱 정해진 어떤 숫자 (i.e. 샘플의 크기 ; sample size) 로 나눠주면 평균이 됩니다. 즉, 바이노미얼의 파라미터 n이 충분히 크다면, 이건 n개의 베르누이 시행의 평균에 고정된 상수를 곱한 것이기 때문에 역시 정규 분포로 근사한다는 뜻입니다.
여기에 더해 1-1에서 보여 드렸듯, 포아송 분포도 바이노미얼로부터 유도해 냈습니다. 그리고 앞서 람다는 샘플 사이즈 n과 사건의 발생 확률 p를 곱한 것으로 이야기했었습니다. 람다와 샘플 사이즈 n이 비례한다는 건데, 그러니 n이 "충분히 크다"는 것은 "람다도 비례해서 충분히 크다" 는 걸 의미합니다. 따라서 람다가 충분히 크다면 포아송 분포가 정규 분포로 근사한다고 할 수 있을 겁니다.

※ 그림은 이렇게 그렸지만, 포아송 분포의 확률 변수는 discrete RV입니다 !
2. 지수 분포 (Exponential distribution)
저번 포스트에서 썼던 문장을 그대로 한 번 더 쓸 수 있을 것 같습니다:
" 먼저 '시행 횟수'에 관한 확률 분포를 봤다면, 그 다음에 따라오는 것은 반드시 '1회 T(성공) 까지 걸린 시간 (Waiting time)' 입니다. "
지수 분포는 포아송 프로세스에서의 waiting time에 관한 분포입니다. "발생 빈도가 람다인 시행에서, 처음 사건이 일어날 때 까지 걸린 시간이 X일 확률" 을 의미하는데, 이번엔 확률 변수 X가 시간이므로 지수 분포는 연속 확률 분포입니다.
유도 과정은 썩 어렵지는 않은 편입니다.
시간이 t일 때 처음으로 사건이 발생했다고 해보겠습니다. 이는 다시 말하면 시간이 0부터 t인 구간에서는 사건이 일어나지 않았다는 거겠죠. 그걸 수식으로 어떻게 쓸 수 있을까요?
포아송 분포의 확률 변수 X에 0을 집어 넣으면 됩니다.
$$ P(T>t) = e^{- \lambda t} \quad ( \because X \sim Poisson( \lambda t ) \Rightarrow f_X(0) = e^{\lambda t} ) $$
그런데 이걸 잘 만지면 지수 함수의 CDF를 찾을 수 있어요.
Reminding :
어떤 CDF \( F_X(x) \) 는 누적 확률을 의미한다는 것, 일전에 소개해 드렸어요.
이걸 우리가 익숙한 확률 기호로 다시 쓰면 아래와 같습니다.
$$ F_X(x)=P(X \leq x) $$
$$ \begin{aligned} P(T\leq t) &= 1 - P(T > t) \\ &= 1-e^{- \lambda t} \\ &= F_T(t) \end{aligned} $$
CDF는 0보다 큰 값을 가져야 하니, t는 0보다 큰 실수여야 할 거예요. 이 구간에 대해서 CDF를 미분하면 지수 분포의 pdf를 얻을 수 있습니다.
$$ \frac{d}{dt}F_T(t) = \lambda e^{- \lambda t} = f_T(t), \quad t>0 $$
요약하면,
$$ X \sim Exp(\lambda) \Rightarrow f_X(x)=\lambda e^{- \lambda x}, \quad x>0 $$
그리고
$$ E(X) = \frac{1}{\lambda}, \; Var(x)= \frac{1}{\lambda ^2} $$
$$ M_X(t) = \frac{\lambda}{\lambda - t} , \quad t<\lambda $$
지수 분포의 MGF와 평균, 분산은 계산을 통해 쉽게 유도할 수 있습니다.
또한 지수 분포도 역시 waiting time 에 관한 확률 분포이기 때문에, 지난 포스트에서 소개해 드렸던 memoryless property가 있습니다.
지난 포스트의 흐름대로 생각해보면, 이 다음에는 n번째 사건이 일어날 때 까지 걸린 waiting time의 확률 분포를 볼 차례인 것 같군요 !
3. 감마 분포 (Gamma distribution)
그래서 다음으로 소개해 드릴 확률 분포는 감마 분포인데... 이름부터 뭔가 거부감이 팍팍 듭니다. 다시 한 번 느끼지만, 통계학은 이름들을 참 못붙이는 것 같아요.
감마 분포는 깊게 소개해 드리거나 뭔가 증명을 보여드리기엔 좀 그렇고, 간단히 소개만 해 드리겠습니다.
이 포스트가 무슨 성적에 들어가는 전공 과목도 아니고 교양(?) 내지 참고용 컨닝페이퍼로 작성하는 건데, 이 친구는 비쥬얼부터 쉽지 않게 생겼어요. 본 전공도 빡센데, 이런 수식까지 외우기엔 저희 시간이 부족하니까요 (물론, 통계학을 자주 접하시면 어쩔 수 없이 외워지게 되긴 합니다).
감마 분포(Gamma distribution ; 보통 그리스 문자 \gamma 가 아닌 영어 Gamma로 표기합니다) 는 두 개의 파라미터를 사용합니다. 알파(\( \alpha \))와 베타(\( \beta \))를 쓰는 책도 있고 여러 가지가 있는데, 저는 \( k \) 와 \( \theta\) 를 사용하겠습니다.
첫 번째 파라미터는 사건의 "k번째 발생" 을, 두 번째 파라미터는 비율(rate)의 역수, 즉 이전까지 봤던 \( \lambda \)의 역수를 의미합니다. 이 때,
$$ X \sim Gamma(k, \theta) \Rightarrow f_X(x)=\frac{1}{\Gamma (k) \theta ^k} x^{k-1} e^{-x/ \theta}, \quad x>0 $$
그리고
$$ k >0, \; \theta = \frac{1}{\lambda} >0 $$
$$ E(X)=k\theta , \; Var(X)= k \theta^2 $$
$$M_X(t) = (1-\theta t)^{-k} = \left( \frac{\lambda}{\lambda - t} \right) ^{k}, \quad t<\frac{1}{\theta} $$
보시다시피 감마 분포의 MGF는 지수 분포의 MGF를 k번 곱한 겁니다.
이는 지난 포스트의 지오메트릭 분포와 NB 분포 사이의 관계와 같음을 의미해요.
자세한 설명은 지난 포스트의 4-1절로 갈음하고, 저희는 저 함수식에 붙은 대문자 감마(\( \Gamma\))가 뭔지 살펴 보도록 할게요.
3-1. 감마 함수 (Gamma function) ; 팩토리얼을 함수 식으로 나타낼 수 있다면?
수리통계학이나 여타 수학 분야에서 종종 접할 수 있는 감마 함수라는 건, 아래처럼 생긴 함수 식들을 총칭하는 말입니다:
$$ \Gamma(k) = \int_0^{\infty} x^{k-1} e^{-x} dx, \quad k>0 $$
이건 또 무슨 식이야... 싶지만, 감마 함수와 관련해서는 우선 아래 특징들만 알고 계셔도 좋을 것 같습니다:
1. \( \Gamma (k) = (k-1) \times \Gamma (k-1) = (k-1)! \) . 즉, 감마 함수의 함숫값은 정확히 결정된 상수입니다.
2. \( \Gamma (0)=1,\; \Gamma (\frac{1}{2}) = \sqrt{\pi} \)
3. 감마 분포의 모양은 감마 함수의 모양과 비슷한데, 이는 적당히 계산을 통해 확률 합이 1이 되도록 만들어 준 것이다.
여담이지만 통계학, 특히 수리 통계학 분야로 들어가시면 이 감마 함수 / 분포와 많이 친해질 수 있습니다.
감마 함수가 필요한 확률 상황이 많이 쓰인다기 보다는, 적분 식을 계산할 때 감마 분포의 확률 합이 1이라는 점을 활용해서 계산을 스킵하는 경우가 많아져서 그렇습니다. 예를 들어
$$ \int_0^{\infty} x^3 e^{-x} dx $$
를 계산할 때, 무작정 IBP(Integration By Part ; 고등학교 수학의 부분 적분) 를 사용해서 적분을 세 번 해도 되지만, 감마 분포를 쓰면 훨씬 빠르고 더 멋지게 답을 구할 수 있습니다.

아마 이 포스트를 보시는 분들께서 수리통계학이나 확률론과 같은 통계학과 저학년 전공 과목을 수강하실 예정에 있으시다면 이런 테크닉을 정말 많이 보시게 될 겁니다. 다항식과 지수 함수가 결합된 형태의 적분 문제는 이제 암산으로 풀 수 있어요.
감마 분포의 또 다른 쓰임은 특정한 경우에 감마 분포가 카이 스퀘어 분포가 된다는 것인데, 이는 추정 파트 혹은 부록에서 간단하게 짚어 드리도록 하겠습니다.
4. 베타 분포 (Beta distribution)
베타 함수를 사용하는 베타 분포는, 어떤 특정한 상황을 가정하고 소개드리는 분포라기 보다는 감마 함수가 나올 때 항상 세트로 붙어 나오는 분포입니다.
아마 바이오 계열에서는 딱히 보실 일이 없을 것 같아 스킵할까 했지만, 교양(?) 느낌으로 소개만 해 드릴게요. 전 유튜브에서 우주 관련 영상이나 초끈 이론같은 물리학 영상을 재밌게 챙겨 보는 편인데 거기서 이 베타 함수가 살짝 엮이긴 하더라구요. 제가 수능을 볼 당시엔 우스갯소리로 생물을 잘 하면 물리를 못하고, 물리를 잘 하면 생물을 못한다는 말이 돌기도 했는데 그래서 그런지 유튜브는 봐도 모르겠습니다만.
먼저 베타 함수(Beta function, 역시 그리스어 대신 영어 Beta 라고 씁니다) 는 이런 식을 말합니다 :
$$ \int_0^1 x^{a-1} (1-x)^{b-1} dx = \frac{\Gamma (a) \Gamma (b)}{\Gamma (a+b)}, \quad a>0,\; b>0 $$
그리고 베타 분포는, 이 베타 함수를 이용해 적분 구간의 합이 1이 되도록 잘 조물딱 거린 함수식으로 이해하셔도 좋겠습니다 :
$$ X \sim Beta(a, b) \Rightarrow f_X(x) = \frac{\Gamma (a+b)}{\Gamma (a) \Gamma (b)} x^{a-1} (1-x)^{b-1}, \quad 0<x<1 $$
이 친구의 평균, 분산, MGF는 ... 아마 보실 일 없을 것 같으니 넘기겠습니다. 저도 외우고 있지 않아요.
베타 분포도 생긴 게 자유분방하게 생겨서 딱 하나로 정형화 할 수 없지만, 그 중 특이한 케이스가 하나 있기는 합니다.
4-1. 균일 분포 (Uniform distribution)
네, 연속 확률 분포 하면 제일 쉬운 케이스로 떠오르는 그 분포 맞습니다.
유니폼 분포는 정의역에 대해 확률 함수로 상수 함수를 갖는 분포를 의미해요.

이런 유니폼 분포는 베타 분포의 한 종류라고 할 수 있어요.
X가 Beta(1, 1)을 따른다면 위의 빨간색 선이 나오는데, 바로 위의 베타 분포 식에 숫자를 대입해 보시면 쉽게 보실 수 있을 거예요.
샘플을 시뮬레이션하는 과정에서 이 유니폼 분포를 쓰는 테크닉이 있기는 합니다만, 당장 저희가 보고 있는 기본적인 가설 검정-추정의 흐름에서는 약간 비껴가기 때문에 유니폼 분포에 관한 내용은 여기까지만 보고 살짝 치워 두도록 하겠습니다.
세 편의 포스트에 나눠 많은 확률 분포를 소개해 드렸습니다.
최대한 쉽게 풀어 보겠다고 하긴 했는데, 전혀 잘 되지 않은 것 같아 마음 한 구석이 조금 아프네요.
그만큼, 이 확률 분포들이 기본적인 친구들이긴 하지만, 무작정 쉬운 내용은 아닙니다. 실제로 보통 기초 통계학에서 다루지 않는 녀석들이기도 하구요. 이 시리즈의 처음부터 딱 이 정도까지가 저학년 통계학과 전공 과목 한 학기 커리큘럼에 거의 근접한 정도이기도 합니다(제가 임의로 추가한 부분들도 있고, 미적분 테크닉이 필요해 통계학 비전공자들에게 불필요하겠다 싶은 내용을 쳐내기도 해서 완전히 동일하지는 않지만요).
다음 포스트부터는 이제 실제로 저희가 하고 싶은 것, '추정(Inference)' 을 소개해 드릴까 합니다.
개인적으로 계획하기에는 기초 통계학의 내용을 좀 많이(?) 넘어가는 걸로 생각하고 있습니다. 고등학교 확률과 통계에서 잘못 배운 추정, 신뢰 구간, 햇 노테이션 (hat notation) 들을 깨는 것 부터 p-value, 95% 같은 유의 수준, 귀무 가설과 대립 가설, 그리고 그들에 대해 일반적으로 오해하고 있는 관점 등을 짚어드릴 예정이예요. 이런 이야기들을 매끄럽게 이어나가기 위해서는 사람 돌아버리게(!) 만드는 통계학의 꽃, 수리통계학의 많은 정리와 요상한 개념들이 필요하지만 깊은 내용들은 빼고, 최대한 한국어로 풀어서 쓸 계획인데, 잘 될지는 모르겠습니다.
그래서 그 첫 번째 이야기로, 추정이라는 과정에 사용되는 여러가지 개념들을 먼저 풀어 소개해 드리는 내용을 준비해 보겠습니다.
'Z-bio stat > Z-기초통계학' 카테고리의 다른 글
| [Z-bio Stat] 8. Bernoulli Trial: Binomial, Geometric, Hypergeometric, Negative Binomial Distribution (0) | 2023.01.10 |
|---|---|
| [Z-bio Stat] 7. 정규분포로 보는 분포(Distribution)의 의미: 분포는 프리셋(preset) 이다 (0) | 2023.01.01 |
| [Z-bio Stat] 6. 데이터와 차원의 표현: 정보의 압축 (0) | 2022.12.29 |
| [Z-bio Stat] 5. 선형대수 표시법: Matrix를 왜 쓰는가? (0) | 2022.12.22 |
| [Z-Bio Stat] 4. 확률 함수 : cmf / cdf / pmf / pdf (0) | 2022.11.28 |



